ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ ОЦЕНОК ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ

Рассмотрим последовательность определе­ния доверительных интервалов для оценок параметров наиболее распространенных распределений.

В § 5.2 была найдена оценка максимального правдоподобия мате­матического ожидания нормально распределенной случайной величи­ны (5.19). Известно F5, 36, 38, 68], что выборочное среднее (5.19) мож­но использовать как оценку математического ожидания для любого распределения, так как в соответствии с законом больших чисел с

увеличением п величина тх стремится к тх.

Если генеральная совокупность бесконечна (в этом параграфе будем считать, что это условие выполняется), то дисперсия оценки тх

D[mx — От = оxln, (5.27)

где ст2д- — дисперсия самой случайной величины.

В общем случае выборочное среднее (5.19) может иметь произволь­ный закон распределения, зависящий от исходного закона случайной

величины X, так как оценка тх — сумма случайных величин лу. Для нормально распределенной случайной величины X выборочное сред­нее является оценкой максимального правдоподобия для тх и как линейная функция от нормально распределенных выборочных значе­ний имеет также нормальное распределение с дисперсией (5.27).

Двусторонний доверительный интервал нормально распределен-

„2

пои оценки тх с математическим ожиданием т,,: и дисперсией от

(5.26) при коэффициенте доверия у в соответствии с (5.5) и (2.96)

л л

тх — и,_т ат < тх <тх + и^от, (5.28)

~ 2

где и, ^ = ы1+ — соответствующая квантиль нормального распре — ~ ~

деления (см. табл. П.4).

Односторонний нижний (верхний) доверительный интервал оценки тх с коэффициентом доверия уі(уг)

Пример 5.1. Пусть при п=9 испытаний по (5.19) найдена оценка матема-

л

тического ожидания тх ~ 3,12 нормально распределенной случайной величины — с дисперсией о — 1. Требуется найти двусторонний доверительный интервал

Л

оценки тх с коэффициентом доверия у = 0,9.

Используя (5.27), найдем среднее квадратическое отклонение оценки

ст = уТ/9 • 1 «s 0,333.

По табл. П.4 определяем квантиль ц)+т = 1,645 и в соответствии с (5.28) получим —jr

3,12 — 1,645 • 0,333 С тх <3,12+ 1,645 • 0,333, или 2,57 « тд. < 3,67, т. е. с вероятностью 0,9 случайный интервал (2,57; 3,67) накроет истинное значе­ние тх.

Обозначим через Дтх половину двустороннего доверительного интер­вала (5.28), отнесенного к среднему квадратическому отклонению <тж случайной величины X. Тогда в соответствии с (5.27) и (5.28)

Ат. х = ат/ах = «щ/ Ип. (5.30)

2 2

Зависимость (5.30), разрешенная относительно п, позволяет найти необходимое число независимых испытаний для подтверждения тре­буемого доверительного интервала длиной 2Дтзстр:

TpJ. (5.31)

Величину лтР округляют в большую сторону до целого числа. Аналогично, длина одностороннего доверительного интервала, от­несенная к ах, в соответствии с (5.27) и (5.29)

Д^!х = % от 1ох = иь V 1 In. (5.32)

Отсюда требуемое число испытаний при заданном Дт^р можно найти по (5.32):

«гр ^(%/ 1х тР)2. (5.33)

Пример 5.2. Найти требуемое число независимых испытаний для полу-

л

чения оценки тх, которая с вероятностью у = 0,9 не отклонилась бы от истин­ного значения тх более чем на 0,6, при 0V = 1.

По условию, Д тХТР = Д тх/ох — 0,6/1 = 0,6.

При у = 0,9 по табл. П.4 находим «|_|_otg == 1,645 и в соответствии с

, 2

(5.31) получим ихр> 1,645а/0,6а « 7,52. Принимаем птр = 8.

Для определения доверительного интервала оценки дисперсии А,

Ох нормально распределенной случайной величины X можно исполь-

Л2

зовать ха-распределение (см. табл. П.1 и П.8). Если оценка ох рас­считана по (5.22) при известном истинном значении тх, то следует ис-

пользовать х2~РаспРеДеление с k — п степенями свободы, а если

Ап

оценка Ох найдена по (5.21), то с k = п — 1 степенями свободы. Двусторонний доверительный интервал оценки среднего квадра-

А

тического отклонения ах (5.22) или (5.21) при коэффициенте доверия •у определяется выражением

ох Y <а*< ох |/ 6/хнл, (5.34)

2 2

где х.2!__ 7 и X2i+T — соответствующие квантили /^распределения,

~Т ~2

определяемые по табл. П.8.

А А

Интервал (5.34) построен так, что нижняя Xi и верхняя /г границы

А

отсекают под кривой плотности вероятности на интервалах (0, /і) и (Хг, °°) площади, равные (1 — у)/2.

Пример 5.3. Пусть в результате п = 21 испытаний при неизвестной вели*

А

чине тх найдена оценка среднего квадратического отклонения ох =1,5 нормаль­но распределенной величины X. Требуется найти доверительные пределы оцен — А

ки ах при коэффициенте доверия у = 0,9.

По k = п — 1 = 21 — 1 = 20; (1 — у)/2 = (1 — 0,9)/2 = 0,05; ((1 + у)/2 = = (1 + 0,9)/2 = 0,95 в табл. П.8 находим квантили У. о 05 3! .4 и Хо Э5 = 10,85.

В соответствии с (5.34) имеем

1,5 /20/31,4 <сж< 1,5 /20/10,85 , или 1,20 < оя < 2,04,

А

Доверительный интервал оценки тх (5. 19) при неизвестном значе­нии дисперсии исходного распределения рассчитывают с помощью распределения Стьюдента (см. табл. П.1 и П.9). Аргументом этого

А ___ А

распределения является случайная величина (тх — /пх)/ k + Мох, а плотность вероятности образуется как отношение нормальной к X2. Распределение Стьюдента при k-^-oo сходится к нормальному, но при малом объеме выборки заметно отличается от него. При неизвест­ном истинном значении 0* двусторонний доверительный интервал оцен-

А

ки тх с коэффициентом доверия у можно представить неравенством

А А АЛ

1ПХ t-(,kOm 01х<^ Шх t-,kOm, (5.35)

где — квантиль распределения Стьюдента (см. табл. П.9);

Л Л

k = п — 1; 0m = ojy п.

При гО> 60 доверительный интервал (5.35) практически совпадает с интервалом (5.28), границы которого вычисляются при известной величине ах с использованием нормального распределения. Интервал (5.35) при прочих равных условиях и п<С 60 является более широким, чем интервал (5.28). Это отражает отсутствие достоверной информации о величине ах.

Л Пример 5.4. Пусть при п — 9 испытаний Найдены оценки? тх = 3,12 и Од. = 1,0 нормально распределенной величины X. Требуется определить довери-

Л

тельный интервал оценки тх при коэффициенте доверия у = 0,9.

По у = 0,9 и А = п — 1 = 8 из табл. П.9 находим /о,9;8 = 1,860 и в соот­ветствии с (5.35) получим доверительный интервал:

1 1

3,12— 1,860 ——- — < т < 3,12-4- 1,860 —— > или 2,50 < т < 3,74.

/9 * х

Заметим, что при тех же условиях доверительные пределы при известной величине Од = 1,0 составляли 2,57 и 3,67 (см. пример 5.1).

Л Л

Односторонний нижний доверительный предел Р, і оценки Р парамет­ра биномиального распределения можно найти следующим образом.

Л

Вероятность получить ровно т отказов в п испытаниях, если вероят­ность успеха в одном испытании Р, определяется выражением (5.10),

Л

а вероятность получить не более т отказов — суммой вероятностей по-

Л

лучения ровно 0, 1,2, …, т отказов, т. е. зависимостью

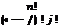
(5.36)

Отсюда искомый односторонний нижний доверительный предел

Л Л

Рін оценки Р определяется уравнением

Л

т

п 1 Л«—і { Л /

(П у) j j j ^ін U pj < 1 .Vi — (5.37)

/=0

Аналогично можно получить выражения для верхнего предела

Л

Р 1в. Заметим, что если коэффициенты доверия односторонних довери-

Л л

тельных интервалов (0, Р1в) и (1, Р1п) равны (yf = у2). то для двусто-

Л л

роннего интервала (Ри, Рв) коэффициент доверия составит 2у( — 1. В табл. П.10 приведены значения пределов двустороннего доверитель-

л л

ного интервала при 2у4 —- I = 0,9 (см. Г7І). Величины Р„ и Рв можно использовать и как односторонние пределы, но при ^ — 0,95.

Пример 5.5. Пусть в результате п = 20 испытаний наблюдался один отказ

Л

(т = 1). Найти двусторонний доверительный интервал оценки вероятности бе­зотказной работы с коэффициентом доверия 2уі — 1 = 0,9 и односторонний ниж­ний доверительный предел этой оценки при — ц = 0,95.

Л Л Л Л

По табл. П. 10 для т = 1 и п — т = 19 находим: Рн = 0,784, Рв = 0,997. Л

Величина Рн = 0,784 будет и односторонним нижним доверительным пределом Ріи приут = 0,95. В соответствии с (5.12) несмещенная оценка вероятности безот­казной работы Р = 1 — 1/20 = 0,95.

Если при биномиальном плане испытаний не было отказов, то

односторонний нижний доверительный предел оценки вероятности безотказной работы можно вычислить по простой формуле. Так как для одного испытания вероятность успеха Р, то в п испытаниях полу­чить подряд успешный исход можно с вероятностью Рп. Если Р ^ 1, то вероятность неполучения отказов в п подряд испытаниях весьма мала (1 — уі > 0). Поэтому можно записать

Нн = 1 — Ті. или Рш = (1 — Ті)’7" . (5.38)

л

а по табл. П.11 определить значения Рін для уі = 0,999; 0,990 ; 0,975; 0,950; 0,900; 0,800.

Число подряд безотказных испытаний /irV, требуемых для под­тверждения одностороннего нижнего доверительного предела Р1в с коэффициентом доверия уь определяется по аналогии с (5.38) выра­жением,

Птр = !°g(l — Yi)/l°gPi„. (5.39)

Заметим, что в (5.39) величина PUt не случайная, так как довери­тельный интервал (Р1и, 1) задан заранее и не связан со случайной оцен-

Л

кой Р. Для определения значений птр также может быть использова­на табл. П.11.

Для уі = 0,9 выражение (5.39) принимает вид

птр = 1/—lg/^ін — (5-40)

Ниже приведены значения требуемого числа подряд успешных испытаний для подтверждения одностороннего нижнего доверительного предела Рін при уі = 0,9:

Рт… 0,50 0,60 0,70 0,80 0,85 0,90 0,95 0,99 0,999 0,9999

«тр… 4 5 7 11 15 22 45 230 2303 23026

В тех случаях, когда надежность близка к единице и в испытаниях

Л

отказов не наблюдалось, по (5.12) получаем оценку Р = 1,0, а по (5.38)

Л

находим нижний доверительный предел Рін с коэффициентом доверия

Л

yt. Наблюдение в п испытаниях т = 0 свидетельствует о том, что ис­тинное значение надежности Р при данном объеме выборки весьма близ-

л

ко к единице и накрывается интервалом (PiH, 1) с вероятностью уь

Пример 5.6. Найти односторонний нижний доверительный предел оценки вероятности безотказной работы изделия с коэффициентом доверия у* = 0,950, если в проведенных 55 испытаниях не наблюдалось ни одного отказа.

Л

По табл. П. 11, интерполируя для п = 55 иуі= 0,950, находим Рін = 0,946. Пример 5.7. Найти число птр подряд успешных испытаний изделия, при котором с коэффициентом доверия yi = 0,999 будет подтвержден нижний одно-

Л

сторонний предел вероятности безотказной работы Ріи = 0,950.

Интерполируя по табл. П. 11 приуі = 0,999 и Ріи = 0,950, находим яТР = 152.

Как известно, биномиальное распределение при <х> сходится к нормальному, однако эта сходимость довольно медленная. Для наи­более важного в практике расчетов надежности случая, когда Р > 0,9, удовлетворительная аппроксимация биномиального распределения нормальным возможна лишь при п> 100 — й 200. При сравнительно

о, Л

малом числе испытании (п = 10 — г — 100) и Р7> 0,9 биномиальное рас­пределение можно описать законом Пуассона, что позволяет с точно­стью практически до третьего знака найти односторонний нижний до-

Л л

верительный предел Р1Н биномиальной оценки Р[см. (5.12)]. В работе [7] предложена следующая аппроксимация точного уравнения (5.37):

Л			Л
	п! fn—j	(i-U«
(п — І) ! j! ґ1н
Й0		/=0 1 ■
	“1-1, = (	(2n —m)(l —

где ai_Tl — (1 — уі) — квантиль распределения Пуассона, определя­емая по табл. П.7.

В соответствии с (5.42) имеем

Р1а = І2/г — т — ^ (т)]/[2п — т + (т)] . (5.43)

л л

Таким образом, по значениям п, т можно найти оценку Р (см. (5.12)]

Л

И ее односторонний НИЖНИЙ доверительный предел Р1Н. Для этого

Л Л

при заданных значениях и т по табл. П.7 находят квантиль (т),

Л

а по (5.43) вычисляют искомую величину Р1н.

Если заменять биномиальное распределение нормальным, то соот-

Л

ветствующий односторонний НИЖНИЙ доверительный предел Р 1н оцен-

Л

ки Р (5.12) в соответствии с (5.29) можно найти в виде

л л

Pin = Р ^ Gp >

где Op TV V Р(1 — P)l(n — 1) — среднее квадратическое отклонение

Л

оценки Р [см. (5.13)].

Пример 5.8. Пусть в результате 20 испытаний (п = 20) наблюдался один отказ изделия. Найти оценку вероятности безотказной работы изделия и ее ниж-

Л

НИЙ односторонний Предел Рщ С коэффициентом доверия Ух = 0,95.

д

По зависимости (5.12) имеем Р = 1 — 1/20 = 0,95. Используя табл. П. 10 ‘Л Л Л

при п — т = 20 — 1 = 19 и т — 1, найдем Р1и = 0,784 (см. пример 5.5).

При отсутствии табл. П. 10, которые имеют три входа: Vi» я — т, т, можно, Л Л

используя табл. П.7 при tn = 1 и 1 —Vi ~ 0,05, найти а,—(1(т) = 4,744.

По (5.43) получим Рш = (2 ■ 20 — 1 — 4,744)/(2 • 20 — 1 + 4,744) = = 0,783.

При аппроксимации биномиального распределения нормальным по (5.13) определяем

ар = "рг0,95 (1 — 0,95)/19 = 0,05.

По табл. П.4 при Yi = 0,95 получим ы0 95 = 1,645 и, подставляя в (5.44), найдем

Р1Н = 0,95 — 1,645 • 0,05 = 0,863.

Из примера видно, что распределение Пуассона практически точно заменяет биномиальное, а нормальная аппроксимация груба. В

л

табл. 5.1 приведены значения Р1н, вычисленное при-р = 0,950 и 0,975,

Таблица 5.1 Значення Л Р1Н для различных коэффициентов доверия п ^1 = 0,950 1, = 0,975 Л Р = 0,900 Л Р = 0,950 Л Р = 0,975 Л Р = 0,900 А Р = 0,950 Л Р = 0,975 0,606 0,555 ю 0,600 0,546 0,736 0,704 0,717 0,784 0,683 0,751 20 0,716 0,783 0,680 0,750 0,786 0,868 0,765 0,852 0,785 0,850 0,886 0,763 0,830 0,868 40 0,785 0,851 0,887 0,762 0,830 0,868 0,821 0,892 0,934 0,806 0,881 0,926 0,824 0,888 0,923 0,810 0,875 0,912 80 0,827 0,889 0,923 0,812 0,877 0,913 0,844 0,909 0,945 0,833 0,901 0,940 0,835 0,897 0,821 0,886 І00 0,836 0,898 0,824 0,887 0,851 0,914 0,841 0,907

Л

оценках Р = 0,900; 0,950; 0,975 и п = 10, 20, 40, 80, 100. Для каждой

л

тройки значений Р, п, в таблице даны последовательно: точное зна­чение, найденное решением уравнения (5.37), пуассоновское прибли­жение (5.41)—'(5.43) и нормальное приближение (5.44). Некоторые

клетки таблицы не заполнены, так как значения т, по которым опре-

Л

делялись оценки Р, принимались целыми числами.

л

Из данных таблицы видно, что в области Р > 0,9, п = 10 ~ 100 пуассоновское приближение практически с точностью до 1—2 единиц третьего знака заменяет точное биномиальное. Нормальное же при-

л

ближение дает завышенные значения Р1п. При использовании нормаль­ного приближения можно рекомендовать в (5.44) вводить поправочный коэффициент Kn, it> зависящий от числа испытаний я и доверительной вероятности

^н=*„,п(£-«Т1<Тя). (5-45)

л

Для п — 10-т — 200 и у4 = 0,90 — 0,99 точность определения Р1н по (5.45) может быть такой же, как при использовании пуассоновского приближения, если поправочный коэффициент находить по зависимо­сти

Кп, ъ = 1 — (І2,80уі — 10,36)/я. (5.46)

В соответствии с (5.46) для yf = 0,950 и у4 = 0,975 имеем:

Дл; 0,950 = 1 — 1,80/я; (5.47)

Дл; 0,975 = 1 — 2,12/я. (5.48)

А

Пример 5.9. В условиях примера 5.8 найти величину Р1н при — ц = 0,95, используя нормальное приближение и поправочный коэффициент (5.46).

В соответствии с (5.47) получим

К21). 0.950= 1 — 1,80/20 = 0,91»

А

На основании (5.45) имеем Рг н = 0 ,91 • 0,863 = 0,785, при точном значении

А

Р1н = 0,784.